乐器评价网

2500年前的一天，古希腊数学家、哲学家毕达哥拉斯外出散步，经过一家铁匠铺，发现里面传出的打铁声响，要比别的铁匠铺更加协调、悦耳。他走进铺子，量了又量铁锤和铁砧的大小，发现了一个规律，音响的和谐与发声体体积的一定比例有关。

尔后，他又在琴弦上做试验，进一步发现只要按比例划分一根振动着的弦，就可以产生悦耳的音程：如1:2产生八度，2:3产生五度，3:4产生四度等等。

就这样，毕达哥拉斯在世界上第一次发现了音乐和数学的联系。

下面这个琴童入门的时值计算，数学不好的话能懂不？

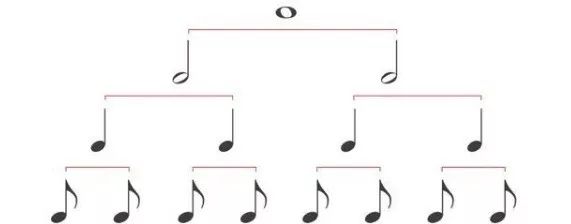
如果学音乐的人数学不好，那肯定掰断了十个手指头也算不清关系大小调和同宫系统。

尽管爱因斯坦、莫扎特和贝多芬都是天才，但他们并不知道自己的大脑比普通人的“大”。现在经过科学实验已经证明，人通过学习音乐和数字可以使大脑中的 “灰质严增加，于是变得更加聪明。

音乐对数学机能的影响在于，音乐与数学之间的联系是因为两者都依赖于人的时空信息处理机能。在弹钢琴的时候，人需要按特定的形式和手指组合来进行复杂的技巧活动，从而弹奏出美妙的音乐。

从信息处理的角度来看，这就是将时间和空间的关系以一种艺术的方式表现出来。因此，心理学家们通过研究所得出的结论是，音乐训练可以提高孩子的时空推理能力，并且因此而促进孩子数学机能的发展。

音乐和数学一样，由人类心智的自由创造，但创造它的逻辑却是客观严谨的。创造出的产物可以无比的严谨、优美并且可以同时兼具高度的独创性和洞察力。

音乐与数学

其实说起数学与音乐的联系，最直观的是，作为记录音乐的乐谱就是以数字为基础的：五线谱以高低音符构筑，犹似数字的级进，简谱所用的阿拉伯数字，从1到7，更体现出了音乐在数字上的奇妙构成。

古希腊数学家、哲学家毕达哥拉斯，他认为，“万物皆数”、“数是万物的本质”。他将黄金分割公式置于“万物”之中，并有一个音乐化的表述：太阳、月亮、星辰的轨道，与地球的距离之比，分别等于三种协和的音程，即八度音、五度音、四度音。

钢琴键盘上的数学

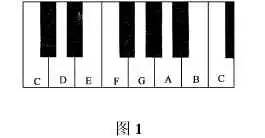
看一下乐器之王 ——钢琴的键盘吧，其上也恰好与斐波那契数列有关。我们知道在钢琴的键盘上，从一个 C 键到下一个 C 键就是音乐中的一个八度音程(如图1) 。其中共包括13 个键，有8 个白键和5 个黑键，而 5 个黑键分成 2组，一组有 2 个黑键，一组有 3 个黑键。2、3、5、8、13 恰好就是著名的斐波那契数列中的前几个数。

注：斐波那契数列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

音乐中的等比数列

如果说斐波那契数在钢琴键上的出现是一种巧合， 那么等比数列在音乐中的出现就绝非偶然了: 1、2、3、4、5、6、7、i等音阶就是利用等比数列规定的。

音乐中的数学变换

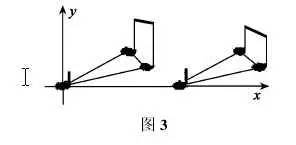
数学中存在着平移变换，音乐中是否也存在着平移变换呢？我们可以通过图 2的两个音乐小节来寻找答案。显然可以把第一个小节中的音符平移到第二个小节中去，就出现了音乐中的平移， 这实际上就是音乐中的反复。把图 2 的两个音节移到直角坐标系中，那么就表现为图 3。显然，这正是数学中的平移。我们知道作曲者创作音乐作品的目的在于想淋漓尽致地抒发自己内心情感，可是内心情感的抒发是通过整个乐曲来表达的，并在主题处得到升华，而音乐的主题有时正是以某种形式的反复出现的。比如，图 4 就是西方乐曲 When the Saints GoMarching In 的主题，显然，这首乐曲的主题就可以看作是通过平移得到的。

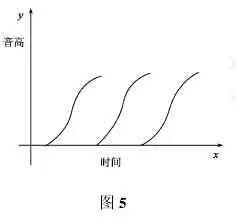
如果我们把五线谱中的一条适当的横线作为时间轴(横轴 x) ，与时间轴垂直的直线作为音高轴(纵轴y) ，那么我们就在五线谱中建立了时间 - 音高的平面直角坐标系。于是, 图 4 中一系列的反复或者平移，就可以用函数, , 近似地表示出来[2] ，如图 5 所示，其中 x 是时间，y 是音高。当然我们也可以在时间 -音高的平面直角坐标系中用函数把图2中的两个音节近似地表示出来。

在这里我们需要提及十九世纪的一位著名的数学家,他就是约瑟夫.傅里叶(Joseph Fourier) ，正是他的努力使人们对乐声性质的认识达到了顶峰。他证明了所有的乐声，不管是器乐还是声乐， 都可以用数学式来表达和描述，而且证明了这些数学式是简单的周期正弦函数的和。

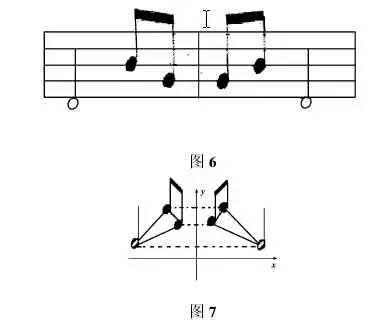
音乐中不仅仅只出现平移变换，可能会出现其他的变换及其组合，比如反射变换等等。图6 的两个音节就是音乐中的反射变换。如果我们仍从数学的角度来考虑，把这些音符放进坐标系中，那么它在数学中的表现就是我们常见的反射变换，如图 7所示。同样我们也可以在时间 - 音高直角坐标系中把这两个音节用函数近似地表示出来。

通过以上分析可知，一首乐曲就有可能是对一些基本曲段进行各种数学变换的结果。

大自然音乐中的数学

大自然中的音乐与数学的联系更加神奇，通常不为大家所知。例如，蟋蟀鸣叫可以说是大自然之音乐，殊不知蟋蟀鸣叫的频率与气温有着很大的关系，我们可以用一个一次函数来表示：C = 4 t – 160。其中 C代表蟋蟀每分钟叫的次数，t 代表温度。按照这一公式，我们只要知道蟋蟀每分钟叫的次数，那么不用温度计就可以知道天气的温度了！

结语

当音乐遇到数学，无序的自然之声成为了有序的音乐之声，让原始声音演化为有律乐音。于是，从玄妙的数学世界走到美妙的艺术世界，数学让音乐更美丽。这也是许多科学家、数学家、文学家热爱音乐的原因吧。